
Converting half adder truth table to a circuit full#
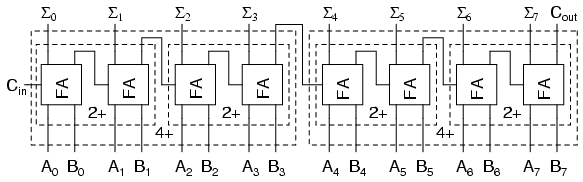
The Full Adder is capable of adding only two single digit binary number along with a. Block diagram Truth Table Circuit Diagram N-Bit Parallel Adder. Then both the outputs SUM and CARRY are 0. From the above truth table the points are evident as follows: If A0, B0 that is both the inputs applied are 0. Let us have a look at the circuit representation of half adder using only NOR gate. The full adder is a three input and two output combinational circuit. To obtain the relation of the output obtained to the applied input can be analyzed using a table known as Truth Table. The figure below represents the circuit representation of half adder by making use of X-OR & AND gate: The above-discussed logic of half adder can also be realized by the help of either NOR or NAND gate only. It can add two one-bit numbers A and B, and carry c. Let’s write the truth table based on this information and general binary subtraction rules. Full adder is developed to overcome the drawback of Half Adder circuit. Since it neglects any borrow inputs and essentially performs half the function of a subtractor, it is known as the half subtractor. Quite similar to the half adder, a half subtractor subtracts two 1-bit binary numbers to give two outputs, difference and borrow. Similarly, for the carry output of the half adder, we need to add Y(A+B) in an OR configuration. So we add the Y input and the output of the half adder to an EXOR gate. The equation for SUM requires just an additional input EXORed with the half adder output. Where X is the equation for EXOR and X’ is the equation for EXNOR.įrom the two equations of SUM and CARRY, we can design the following combinational logic circuit for a full adder.Ĭompare the equations for half adder and full adder. 3 marks ii) Draw the truth table for a half adder circuit and synthesize a circuit using XOR and an AND gate.
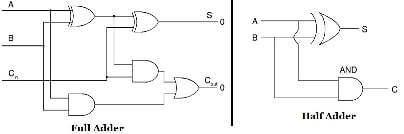
4 marks A B b) i) convert the decimal number 13.687510 into binary form. The Boolean expression of Half Adder circuit is-SUM A XOR B (A+B) CARRY A AND B (A. a) For the logic circuit shown, through reasoning, determine the required input condition (A, B, C) in terms of Os and Is to make the output X1. SUM = A’B’Y + A’BY’ + ABY + AB’Y’ = Y(A’B’+AB) + Y'(A’B+AB’) = YX’+Y’X = This is the construction of Half-Adder circuit, as we can see two gates are combined and the same input A and B are provided in both gates and we get the SUM output across EX-OR gate and the Carry Out bit across AND gate.


 0 kommentar(er)
0 kommentar(er)
